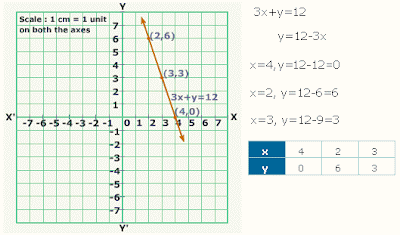
Sine graph generator

Sine graph is the periodic with period 2`pi` .They wriggle back and forth between -1 and 1 in a smooth way. Sine starts at 0 and goes up to 1 .Sine graph generator produce the sinusoidal wave. The sine function graph usually how to find phase sift, period, amplitude for the equation

Sine graph generator following conditions produced y = sinx ,  Domain (− ∞, ∞) , Range [− 1, 1] , Principal domain (−π / 2,π / 2)

Sample Problem for Sine Graph Generator:

Example 1:

 Draw the amplitude for given question y=a sinx for various values of  a.

Solution:

For sine is how far the graph gets away from the x-axis, so it is called the amplitude.

Y=a sinx ,  where a=1,2,3 0.5,0.2

See the given  Sine graph  generator

For sine is how far the graph gets away from the x-axis, so it is called the amplitude.

Y=a sinx    a=2 , -2

See the given  Sine graph  generator

y= 2 sinx, -2sinx

Example 2:

 Draw the amplitude for given question y= sinx for various values of  a.

Solution

y=sinx where x values follows
 x =1, -1
see the sine graph generator

Example 3:

Show that Periods other than 2pi is a little harder; because there is a lot that the graph does in the course of its period. P=2`pi` /b

Y=sinbx where b=1,2,3,0.5

solution:

See the given  Sine graph  generator

Practice Problem for Graphs of Sine Generator:

1. Graphing the amplitude for given question y=d sin2x for various values of d

Answer: d values 1,2,3,1.5,4

2. Graphing the period of given question y= sinbx for various values of b

Answer: b values 1,2,3,1.5

3. Graphing sine periods for y= sinbx values of b and d are;

Answer: b=1,2,3,0.5

4. Graphing the amplitude for given question y=t sin3x for various values of t

Answer: t values 1,2,1.5 0.5,0.3.

Binary System and Introduction

What are Binary Numbers
In the word Binary, ‘Bi’ means two, so a system of numbers which involves only two digits is called binary system. The two binary numbers used are ‘1’ and ‘0’. The binary system works in the same way as the decimal system which consists of ten digits which are 0 to 9, in case of binary system there are only two possible digits 1 and 0. Any number which is expressed in the binary system would be a combination of the two digits, 1 and 0. It is mainly useful in the field of technology.  In an electrical circuit we have only two options which are ‘on’ and ‘off’ and hence based on this the binary system plays an important role in all the communications which take place inside a computer. In a decimal system the place values are ones, tens, hundreds, thousands, ten thousands and so on. These values can be written as power of 10 which would be 10^0, 10^1, 10^2, 10^3, 10^4 and so on. In the same way the binary system starts from the right and proceeds towards left the difference being the base is 2.

Binary Numbers Chart can be given as below
2 raised to power zero = 2^0=1
2 raised to power one = 2^1=2
2 raised to power two= 2^2=4
2 raised to power three=2^3=8
2 raised to power four = 2^4=16
2 raised to power five= 2^5=32
2 raised to power six = 2^6=64 and so on, in general it can be considered as 2 raised to power x = 2^x
For example, let us consider a binary number 1011 and convert it into decimal form
Binary conversion: 8   4   2    1
      Decimal form:  1   0   1    1
1011(base 2) = 1x(8) + 0x(4) + 1x(2) + 1x(1) = 8+0+2+1=11(base 10)

List of Binary Numbers are as follows
0000=0; 0001=1; 0010=2; 0011=3; 0100=4; 0101=5; 0110=6; 0111=7; 1000=8; 1001=9; 1010=10 and so on.
Subtracting Binary Numbers
While subtracting binary numbers the following are the facts to be remembered:
0 – 0 =0 ;  1 – 0 = 1; 1 – 1= 0 and 10 – 1 is equivalent to 2 – 1 = 1 in binary system
Subtract 1011 from 10101.

0110 0110 1
-  1   0 1 1
__________
          1  0 1 0        
(1 -1 =0; 10 – 1 =1;0 – 0 = 0; 10 – 1 = 1 and 0 = 0 which gives 1 0 1 0)
Binary number      10101   -    1011 = 1010
Decimal equivalent   21       -       11   =10

Absolute Values

In algebra and in vectors we come across numbers in negative directions although the magnitudes of such quantities have no signs or supposed to be positive.  Let us take a closer study.



What is Absolute Value in Math
Let us consider the numbers 5 and -5. Algebraically, they are not same. But when you plot these numbers on a number line, they are no doubt on the opposite sides of the origin 0. But they are at the same distance from the origin. That is -5 is also 5 units away from the origin on a number line. Hence considering only the fact of ‘how far’, we can say that the absolute value 0f -5 is 5.
Thus we can define that an absolute value of a number is only its physical value and hence it is always referred as positive. Symbolically the absolute value of a variable ‘x’ is denoted as lxl and it is always equal to + x.

Finding Absolute Value
As explained earlier an absolute value of a number cannot be negative. Thus, the easiest method of finding absolute value of a number is just consider the number only, ignoring the sign before it. That is for finding absolute value of -10, just consider only the number 10. That is l-10l = 10.

Limit of Absolute Value
Since the absolute value of a variable is always positive, the upper limit of the absolute value is infinity. However, because an absolute value can never be negative, it cannot cross below 0. Therefore, the lower limit of absolute value is 0. Thus the limit of absolute value of a variable can be expressed as [0, ∞).

Absolute Value Practice
The concept of absolute value is important. For example, A is situated 10 miles from his office and B is situated 5 miles from the same office but exactly in the opposite direction. Now to calculate the distance between A and B, we cannot algebraically say 10 + (-5) = 5 miles or 5 + (-10) = -5 miles. Here you need to apply the absolute value practice and say the distance is l10l + l5l = 10 + 5 = 15 miles.

Properties of Absolute Values
The important properties of absolute values are,
lxl = x for x ≥ 0, but = -x for x < 0.
If lf(x)l = a then there can be two cases. That is f(x) = a and f(x) = -a.
Suppose lf(x)l + a = b and if a > b, then there is no real solution to the equation.

How to Draw Line Plot?

What is a Line Plot in Math?
The definition of a line plot states that it is a graphical representation of frequency of occurrence of each and every data on a data line. Line plot is graphically represented using some marks such as x or dot.

How to do a Line Plot?
A line is drawn with the data values marked in it as we mark values in the x axis of the graph. The number of occurrences of the data values is marked above the number line individually as the variable x to make a Line Plot.  So the number of “x” marked vertically above each data value shows the number of occurrences of the data value in the given data set. Thus this gives the details of how frequently a data value occurs in the data set.

Example of a Line Plot
Let us consider the marks scored by Students of grade VII in their exam.  Let us assume that there are 10 students in the class and the maximum mark they can score is 100. The marks scored by the ten students are 90, 99, 76, 89, 55, 86, 98, 68, 40, and 35 respectively.

Note that the school follows the grade system as shown below:
• The marks 90-100 will lie in grade A
• The marks 80-89 will lie in grade B
• The marks 70-79 will lie in grade C
• The marks 60-69 will lie in grade D
• The marks 50-59 will lie in grade E
• The marks below 50 are considered as ‘fail’ and they will lie in grade F.

Now let us map the students’ marks in the above grade range:
• The marks lying in grade A are 90, 99, and 98
• The marks in grade B are 89, and 86
• The mark in grade C is 76
• The mark in grade D is 68
• The mark in grade E is 55
• The marks in grade F are 40, 35

From this analysis, we can see that three students have scored grade A, two of them have scored grade B, one student each have scored the grade C,D and E and two students have failed and obtained grade F.  Now, let us mark the line plot with the values A, B, C, D, E, and F:

x
x x x
x x x x x x

<--------------------------------------------------------->
| | | | | |
A B C D E F
Grade
The line plot drawn above gives the graphical representation of the frequency of the occurrence of data in every grade.

Examples of Complementary Angles

What are Complementary Angles?
Two angles are said to be complementary angles, if the sum of the two angles measure 90 degrees.  Thus we can say that two complementary angles together from a right angle measuring 90 degrees. But these two angles need not necessarily be adjacent angles i.e. next to each other.

Example of Complementary Angles
One of the best examples of complementary angles can be seen in right angled triangle.  In a right angled triangle, one angle is the right angle. It is a fact that the sum of all the three angles in a right angle is equal to 180 degrees. Thus, it is clear that the sum of the other two non-right angles will be equal to 90 degrees.  This means that the two non-right angles in a right angled triangle are complementary angles. In other words, we can say that these two angles complement each other.

Some of the other examples of complementary angles are:
55 degrees, 35 degrees
40 degrees, 50 degrees
67 degrees, 23 degrees

How to Solve Complementary Angles?
Now let us see how to find complementary angles.  As we know the definition, finding complementary angles is very easy by applying the definition. If the value of one angle is given, then another angle complementary to that angle is found out by subtracting the given value from 90 degrees.

Example 1:
Consider two angles which are complementary to each other.  If one of the angles is 48 degrees, find the other angle.

Solution: If x is the unknown angle, then 48 added to x will give 90 degrees.  Therefore, x is given by subtracting 48 from 90. i.e., X = 90-48 = 42 degrees.
Therefore, the other angle is 42 degrees.

Some Complementary Angles Problems will be in the form of slightly confusing word problems.

Example 2:
If one of the complementary angles is six more than twice the other angle, find the angles.

Solution:  If the variable Y is considered as one angle measure, then, as per the given statement, the other angle is given by 2Y+6. We know that the sum of the two complementary angles is 90 degrees.  So,
Y+2y+6 = 90
3y = 90-6
Therefore the value of Y will be obtained if 84 are divided by 3. Thus, the value of Y will be 28. If y = 28, then the second angle will be (2*28) + 6 which results in the value 62. Thus, the measures of the angle are 28 and 62.

Free Math Help

Plenty of students find it necessary to find good math help in order to understand the subject and get good grades. Math does not come easily to all and while the subject itself is fairly simple, different students understand it in different ways. Basic math skills are necessary since people use them all the time. Many occupations require an understanding of math or at least specific areas of math.

To learn math effectively, study well right from the beginning. Understanding concepts as and when they are covered, helps students retain them longer. Since each lesson in math builds on what was taught earlier, this ensures that students understand what they are taught as they move further into each topic or chapter.

Going through the lesson before class enables students to get the most out of each class. Even if you don't understand what you are reading, hearing the same thing again will make it much clearer in your mind. It will also enable you to ask better questions and jot down good points. Make it  a habit to go back and study what you have covered in class the very same evening, when it's still swimming around in your memory.

There are a lot of math resources at students' disposal, especially on math help websites. Make use of free math help to learn concepts and get ahead in the subject. Math resources online consist of free worksheets, games and quizzes. There are any number of tutorials covering all the topics in school and college level math, written in simple terms and illustrating each concept with plenty of examples.

Online calculators are very useful tools which can give you the answer for just about any type of question. If you're stuck with a problem, try using any of the free online calculators to get the answer immediately. It is also a great way to cross check your homework and make sure you have everything right. Students can also enlist the help of live tutors who will solve the problem and send you the steps to the solution as well. Practice is key to getting good grades in math and online worksheets provide students with plenty of options to choose from. All the sites provide the answers to their worksheets, with some providing the complete solution too.

Practice of statistics

Statistics in the plural are statistical facts systematically together with some definite object in view, in any field of enquiry, whatsoever of observation, measurement or experiment; for example, statistics of the population of a country, males and females, refugees, births and deaths, heights and weights, income and expenditure, food production, etc. The statistics deals with every aspects of this, consists not only the set, analysis and interpretation of data. The statistics is a technique used to obtain, analyze, summaries, compare and present the numerical data. In this article, example problems and practice problems for learning practice statistics exam is given.

Example Problems for Practice of Statistics:-

Example Problems for learning practice Statistics exam are given below:

1) In statistics the daily maximum temperature recorded in degree C. At New york during the first week of July, 2005 was as under, 39, 37, 38, 28, 30, 35, and 36. Find the mean temperature recorded.

Sol:-

Mean temperature = sum of observations / no of observations

= `(39 + 37 + 38 + 28 + 30 + 35 + 36) / 7`

= `243 / 7`

= 34.7 degree C.

2) find the arithmetic mean of the numbers 3, 0, -1, 7, 11 in statistics.

Sol:-

Mean = sum of observations / no of observations

= `(3 + 0 + (-1) + 7 + 11) / 5`

= `20 / 5`

= 4.

3) In statistics what is the median weekly salary of worker in a firm whose salaries are Rs. 84, Rs. 60, Rs. 50, Rs. 40, Rs. 45, Rs. 42, Rs. 38, Rs. 65, Rs. 71?

Sol:-

1) first arrange the salaries in order: Rs. 84, Rs. 71, Rs. 65, Rs. 60, 50, 45, 42, 40, 38.

2) Next, count the number of salaries. It is 9.

The fifth salary (Rs. 50) has the four salaried which are less than it and four salaries above it. Therefore, Rs. 50 is the middle or median salary.

4) Find the mode for the following data 52, 58, 58, 58, 65, 73, 73, 73?

Sol:-

Here 58 and 73 repeated three times.

So 58 and 73 are two modes.

Practice Problems of Statistics:-

Practice problems for learning practice statistics exam are as follows:

1) Find the arithmetic mean of the numbers 4, 2, 1, 0, 7, 10.

Answer: 4

2) Find the median salary of the following salaries of worker: Rs. 56, Rs. 89, Rs. 121, Rs. 38, Rs. 98, Rs. 70, Rs. 70, Rs. 72.

Answer: Rs. 71.

3) Find the arithmetic mean of the numbers -2, -1, 0 , 1, 4 , 10.

Answer: 2

4) Find the mode of the numbers 10, 11, 12, 12, 14, 15, 15.

Answer: 12 and 15

Exterior angles of polygons

Definition:
For any polygon, the angle formed between any one side of the polygon extended and the next consecutive side is called an exterior angle of that polygon.  See the figure below:

The sum of an internal angle and its corresponding exterior angle is always 180 degrees. In other words the interior angle and the exterior angle of any polygon are supplementary to each other.

A polygon has as many numbers of exterior angles as interior angles. The following figure shows the exterior angles of a pentagon.

Exterior angles theorem:

The exterior angles theorem can be stated as follows:
“The sum of exterior angles of a polygon is always 360 degrees. “
The sum of exterior angles does not depend on the number of sides of the polygon. The sum of interior angles would be different for different polygons. But the sum of exterior angles of a polygon is always 360 degrees.

Proof of the above theorem:

We know that the sum of the interior angles of a triangle = 180 degrees
The sum of interior angles of a quadrilateral = 360 degrees
The sum of the interior angles of a pentagon = 540 degrees
Therefore the sum of interior angles of a polygon of n sides = (n-2)*180 degrees
Therefore the measure of each interior angle = (n-2)*180/n degrees
Since each interior and its corresponding exterior angles are supplements of each other,
Therefore the measure of corresponding exterior angle = 180 - (n-2)*180/n
Therefore the sum of n such exterior angles
= n*[180 - (n-2)*180/n]
= n*[180n – 180n + 360]/n
= 180n – 180n + 360
= 360 degrees
Hence it is proved that irrespective of the number of sides of the polygon, the sum of exterior angles is always 360 degrees.

Exterior angles of a polygon formula:
The formula for the sum of interior angles of a polygon is
= (n-2)*180 degrees

Therefore each of the interior angle would be
= (n-2)*180/n degrees

Therefore the corresponding exterior angle for that polygon would be:
= 180 - (n-2)*180/n degrees

Thus the formula for finding the measure of each exterior angle of an n sided regular polygon is
180 - (n-2)*180/n degrees

Frequency table math

In statistics frequency table refers to the tabular representation of frequencies of a sample. The frequency distribution of a sample can be represented in three ways: (a) Textual representation, (b) tabular representation and (c) diagrammatic representation.

(a) Textual representation: This method comprises presenting data with the help of a paragraph or a number of paragraphs. The official report of an enquiry commission is usually made by textual presentation. The merit of this mode lies in its simplicity and even a layman can present data by this method. This method is however not preferred by statisticians simply because it is dull monotonous and comparison between different observations is not possible in this method.

(b) Tabular representation: We can define frequency table as a systematic presentation of data with the help of a statistical table having a number of rows and columns and complete with reference number, title, description of rows as well as columns and foot notes, if any. This method is any day better than the textual representation because it facilitates comparison between rows and columns. Complicated data can also be represented using a frequency table. To be able to make a diagram for the distribution we first need the data in tabular form. Only then can we convert it to a bar chart or a pie chart. All other parameters such as mean, median, mode, standard deviation, regression analysis etc are not possible unless we have the frequency distribution table.

Example of a frequency table:
The production of rice in a particular region for each year starting from the year 2001 to the year 2007 is given in the frequency table below:

Year	Quantity in MT (Metric tons)(frequency)
2001	25
2002	30
2003	32
2004	36
2005	35
2006	35
2007	37

In the above frequency table example we see that it is relative easy to understand the data. By merely looking at the table we can say that the production in the year 2004 was 36 MT. Also it is fairly simple to calculate the mean, median mode etc as well. Thus we see that representing frequency distribution in tabular has many merits.

(c) Diagrammatic representation of data: Another alternative and attractive representation of statistical data is provided by charts, diagrams and pictures. The various forms of diagrammatic representations are bar chart, histogram, pie chart, etc.

Concepts of Trigonometric Equations

In this article we have to discuss about various trigonometric equations. Before this we have to know about trigonometric identities. In mathematics trigonometric identities means which involves trigonometric functions and they show right value for every single variable. In other way we can also say that, geometrically these are the identities which involve some functions with one or more angles. They are also triangle identities which involves angle as well as side length of triangles. These identities are very useful when we solve the trigonometric-equations. One example of these identities is integration by substitution method.

Now we come to trigonometric-equations. An equation means algebraic functions written by using sum and difference formula. Similarly trigonometric-equations also contains algebraic equations but with trigonometric functions of the variables. If they contain only such functions and variables, then in solution we have to find an unknown constant which is an argument to a trigonometric function. Basically there are fundamental forms of trigonometric-equations, they are

1. Sin X=n
2. Cos X=n
3. Tan X=n
4. Cot X=n
5. Cosec X=n
6. Sec X=n

Where (n) is a constant. Now the equation sin X=n, solved only when (n) lies between the interval [-1, 1]. Suppose n comes under the interval then we need angle. After using some identities we can solve the equation. Similarly for cos X=n solved only when (n) lies between [-1, 1]. Next procedure is same. For equation tan X=n and cot X=n, (n) should be any real number. For equations cosec X=n and sec X=n, these equations can be solved by converting in other basic equations such as (cosec x=1/sin x) and (sec x=1/cos x).

Some other basic form of trigonometric-equations is (Asin x+ bcos x=0). To solve trigonometric equations using various relations between the trigonometric functions, we have to convert trigonometric-equations in a form such that value of one of the trigonometric functions of the desired variable can be determined. The roots of these trigonometric functions can be found by using inverse trigonometric functions. For solving trigonometric equations like (Asin x+bcos x=0), we have to convert this equation into basic form of equation and then using various trigonometric identities we can solve the equation. We separate this equation into real part and angle part.

Trigonometric equations solver means a process by which result can be displayed.  It can find all the solutions. The result shown first in the form of radians and then in decimal form. They show the results also in form of degrees. By using trigonometric equations solver we can solve equations easily.

Mean Median and Mode

What is the definition of mean median and mode?
Mean is a parameter of central tendency measure. The central tendency measure indicates the average value of data, where the term average is a generic term used to indicate a representative value that describes the general centre of data. Mean for raw data and for grouped data. For grouped data it is known as frequency distribution. Mean is the central value of the distribution in the sense that positive and negative deviations from the mean balance each other. It is a quantitative average.

Median is the central value of the distribution in the sense that the number of values less than the median is equal to the number of values greater than the median. So, median is a positional average. Median is the central value in the sense different from the arithmetic mean. In case of the arithmetic mean it is the numerical magnitude of the deviations that balances but, for the median it is the number of values greater than the median which balances against the number of values of less than the median.

Mode is defined as the value of the variable which occurs most frequently. Mode is for both raw data and grouped data. In raw data the most frequently occurring observation is the mode that is data with highest frequency is mode. If there is more than one data with highest frequency then each of them is a mode. Thus we have unimodal means single mode, bimodal means two mode and trimodal means three modes data sets. In grouped data mode is that value of (x) for which the frequency is maximum. If the values of (x) are grouped into the classes such that they are uniformly distributed within any class and we have a frequency distribution than we calculate maximum frequency by using formula.

What is the mean median mode in math?
Now we discuss about what does mean median mode mean in math. There are some formulas in math for mean median and mode.
For raw data mean= [∑x/n], x is refers to value of observation, n is the number of observations.
For grouped data mean= [∑fx/∑f]
Median= [(n+1)/2]
Mode=L+ [f0-f1/2f0-f1-f2]*h, L is lower limit, f0 is largest frequency, f1 is preceding frequency, f2 is next frequency and h is width.
Now, How to find the mean median and mode. Suppose we have given some problem then to find mean median and mode we can use above formula, by using formulas we can get the results.

Understanding the box and whisker plot

Box and whisker plot definition:
The basic assumption in statistics is that a set of data has a central tendency. That means the number of the data are distributed around some central value. The box of the box-whisker plot takes care of the middle half observations of the data. So we can define the box-whisker plot as a diagram that represents the tendency of data to centre on the median.

Box and whisker plot examples:
The following pictures show box and whisker plot of various data sets.

Shown above is a box-whisker plot of weight in pounds of players.

Shown below is a box- whisker plot of the length of fish in a particular lake:

From the plot we can see that the median length is 12 cm. The smallest fish has a length of 5 cm, the longest fish is 20 cm long. Most of the fishes lie between 8.5 to 14 cm in length, where 8.5 is the lower quartile and 14 cm is the upper quartile.

How to make a box and whisker plot:
Step 1: Arrange the data in ascending order from the lowest to highest value.

Step 2: Find the median of the data. For a data of n observations, median = ((n+1)/2)th observation if n is even and if n is odd then median = average of (n/2)th and ((n+2)/2)th observation. So if number of observations = 11 then (11+1)/2 = 12/2 = 6th observation is the median. But if number of observations is 14, then average of 14/2 = 7th and (14+2)/2 = 16/2 = 8th observation would be the median.

Step 3: The median that we found above has now divided the data into two halves. Now to further divide each of the half into two quarters, we need the 1st and the 3rd quartile values. Suppose the median is the mth observation. Then the middle value between the 1st and the mth observation would be the 1st quartile and the middle value between the mth and the last observation would be the 3rd quartile. They are denoted by Q1 and Q3.

Step 4: Now  you have these three values, Q1, M (= median) and Q3. We also have the lowest and the highest observation, X1 and Xn. So we now have 5 points. We make a number line using suitable scale and mark these 5 points and draw a box around the Q1 to Q3. That is our box and whisker plot.

Step by step math solution

Mathematics is used throughout the world and it is an essential tool in many fields like natural science, engineering, medicine, and the social sciences. "Mathematics" is the Greek word its gives the meaning of learning, study, science, and additionally came to have the narrower and more technical meaning "mathematical study", even in Classical times.

Step by Step Math Solutions - Method to Solve:

There are many formulae abounded for solving math problem step by step One of the most important formula is P.E.M.D.A.S. It is nothing but the operations done in the problems solving in math. They are

• Parenthesis
• Exponents
• Multiplication
• Division
• Addition
• Subtraction

Step 1: First perform the operations inside a parenthesis.
Step 2: Now solve the exponents
Step 3: Then multiplication and division is done from left to right
Step 4: Then addition and subtraction is done from left to right

Step by Step Math Solutions - Example Problems:

Step by step math - Problem 1:

Solve the equation step by step

X + 6 = 8

Solution:

It is one step equation

Subtract 6 on both sides

X + ( 6 - 6 ) = (8 - 6)

X = 2

Step by step math - Problem 2:

Solve the equation step by step

4x + 2=18

Solution:

Subtract 2 on both sides

4x + (2 - 2) = 18 - 2

4x = 16

Divide by 4 on both sides

`(4x)/4` = `16/4`

X = 4

Step by step math - Problem 3:

Find the value of x step by step

6x - 8 = 4 x -10

Solution:

Subtract 4x  from both sides of the equation

2x - 8 = - 6

Add 6 to both sides of the equation

2x = 2

Divide both sides by 2:

x = 1

The answer is x =  1

Step by Step Math Solutions - Probability Problems:

Step by step math - Problem 1:

A fair coin is tossed two times. What is the probability of getting at least one heads.

Solution:

Let A = be the event of getting at least two heads

Let S = Sample Space which refers to the total number of probable outcomes.

S = (HH, HT, TH, TT) =4

A = (HT, TH) =2

P (A) = `2/4` = `1/2`

The probability is `1/2` .

Step by step math - Problem 2:

Consider a die is rolled; calculate the probability of in receipt of odd numbers?

Solution:

There are six different outcomes 1,3,5,7,9,10,12,14,16,17,18

n (A) = 6, total number of odd numbers occur 6.

n (S) = 11, total number of outcomes is 11.

Probability of the event A happen = P (A) = n (A) / n(S) = `5 / 11` = 0.45.

Probability of the event A does not happen = P (A') = 1 – P (A) = 1 - 0.45 = 0.55.

Circle Division

A circle is a closed curve. The points on the circle are equidistant from the center of the circle. A circle creates 2 regions, the interior of the circle is one region and the exterior is another region.

A circle can be divided into equal or unequal parts. The division can be accomplished by straight lines or curved lines. With every nth line the circle gets divided into n+1 parts, meaning with one line circle can be divided into 2 parts, with nth line circle can be divided into n+1 parts assuming that the lines do not intersect.

Circle Division Term in Maths:

A circle division can be accomplished by using a straight line or a curved line. As we are not considering the area calculation for this discussion, let us restrict ourselves to straight lines for the purposes of this study.

The straight line that joins a point on the circumference of the circle to another point on the circumference of the same circle is called a chord. A chord divides the circle into 2 parts.

Consider several chords on the circle and suppose some or all of the chords intersect. Then it is found that the number of area regions that the chords cut the circle into is always more than the number of chords passing through the circle.

Here is an example

The above is popularly known as the cake cutting example.

In the first picture, one chord divides the circle into 2 parts.in the second picture, two chords divide the circle into 4 parts, in the third three chords divide the circle into 3 parts and the forth diagram 4 chords divide the circle into 11 parts.

Here you see that the first cut creates 1 new region (1+1)

The second cut creates 2 new regions (2+2)

The third cut creates 3 new regions (4+3) and the 4th cut creates 4 new regions (7+4)

This is mathematically represented as

F (n) = n + f (n-1)

Conclusion for Circle Division:

Circle division is an important study in geometry that gives several clues for practical applications. There are several theorems and postulates that delve deeper into circle division and provide new insights into this area of study.

Frequency and Frequency Table

Frequency table, it comes under the category of statistics. First we see about frequency. The frequency of a given table or data is that how many times the value occurs in table or data. For example, suppose in a class five students are score sixty marks in mathematics then the score of sixty is said to have frequency of five. Frequency means range of values also and the frequency of any data is denoted as (ƒ).

What is a frequency table?
A frequency table contains sets of collected data values. The arrangement is such that the magnitude of collected data values is in ascending order along with the corresponding frequencies. Now frequency table definition in other way is that it is a list of quantity in ascending order and list shows the numbers how many times each value occurs.

How to make a frequency table?
Here we understand the procedure of preparing A frequency table. For this we follow some steps. In step one; we make a table with three columns. In these three columns, first columns shows the marks and marks are arranged in ascending order means start from the lowest value. The second column shows tally marks. It means put corresponding tally in front of marks. When all values listed then make horizontal lines for all the values. Third column shows frequency, count the value of frequency for each mark and write in third column. Finally the frequency table is constructed.

The frequency table is different for different types of problems. Sometimes in problems range values is given with no of students and cumulative numbers. When we make frequency table for this type of problem then in first column we write range value in ascending order. In second column we write number of student which comes under the corresponding range. In third column we write cumulative numbers then we solve the problem.
Always i find probability distributions is very hard for me. If you do feel the same watch out for my coming posts.

How to do a frequency table?
We start with simple example. Suppose we have a frequency table with two columns. In first column marks(20-30, 30-40,40-50,50-60, 60-70) is given and in second column frequency(2,4,3,5,7) is given. Frequency column represent the number of students who scored marks in particular range of frequency. We have to calculate the number of student who gets fifty plus marks. Fifty plus marks comes in 50-60 and 60-70 range and their corresponding number of student is 5 and 7. So the answer is 12 students.

Integral properties and definition

In this article first we define Integration, in mathematics it is an important concept. Its inverse definition is also equally important. Integration is one of the main operations from two basic operations of calculus. In simple form we can define that integration means to calculate area. Now we define mathematically, suppose we have a given function (f) with real variable (x) over an interval [a, b] for a given real line, then we expressed this function as ∫f(x) dx. Integration means calculation of area of the region in XY-plane, which is bounded by the graph of function (x). Area above from the X-axis adds the total value and area below the X-axis subtracts from the total value.

The term integrals also known as antiderivatives. Suppose we have a given function is (F) and derivative of this function is (f). In this case it is known as indefinite integral and can be expressed as ∫f(x) dx. The notion of antiderivative are basic tools of calculus. It has many applications in science and field of engineering. Integral is an infinite sum of rectangles of infinite width. Integral is based on limiting procedure of area. Line integral means function with two or three variables where closed interval are replaced by any curve. Curve may be made in any plane or space. In surface integral in place of plane a short piece of surface is used.

There are various integral properties; integral properties are for the definite notion of antiderivative based on the certain theorems. First theorem is, suppose M(x) and N(x) are two defined functions. They are also continuous function in interval [a, b], then we have linearity property for the notion of antiderivative which can be expressed as
∫ [M(x) +N(x)] dx= ∫M(x) dx + ∫N(x) dx
∫a. M(x) dx= a∫M(x) dx. a is an arbitrary constant and we carry out the constant term from the function.
Second theorem is, suppose function f(x) is defined which is continuous in closed interval [a, b], then we have some special property of integral such as…
∫f(x) dx= 0, when limit are same.
∫f(x) dx= ∫f(x) dx+∫f(x) dx, when limits are divided between interval s like a to c and c to b.
∫f(x) dx= -∫f(x) dx, when upper limit becomes lower limit and lower limit becomes upper limit.

There are many integral types such as definite integral in which function is continuous and define in a closed interval. Other types are indefinite integrals, surface integrals, double integral known as Green’s theorem, triple integrals known as Gauss divergence theorem and line integrals

Graphing Trig functions

Sine graph equation:
The general form of a sine function is like this:
Y = sin x.
As we already know, sine is a periodic function. The period of a sine function is 2 pi. That means each value repeats itself after an interval of 2𝛑 on the x axis. The range of the sin function is from -1 to 1. So the value of sin x would not exceed 1 and would not go below -1 at any point. To be able to plot the graph of the function, let us make a table of values of the sine function.

The graph of the above table would look like a wave.

Cosine graph equation:
Just like the sine function, the cosine function is also periodic. The parent cosine function would be like this:
y = cos x
Similar to the sine function, the range of the cosine function is also from -1 to 1. The period of the cosine function is also 2𝛑. That means that the value of the function repeats itself after an interval of 2𝛑. To be able to plot the cosine function now let us make a table of values of cos.

The graph of the function would look like this:

How to graph tangent functions?

The tangent function is also a periodic function. However the period of the tangent function is 𝛑. That means the values repeat itself after an interval of ?? on the x axis. The range of the tangent function is –inf to inf. That means that the tangent function can have any real number value. Just like how we did for the sine and the cosine functions, for plotting the tangent function also we shall make a table of values.

Properties and derivatives of Logarithm functions

Definition of logarithmic function: For any positive number a is not equal to 1, log base a x = inverse of a^x. The graph of y = log x can be obtained by reflecting the graph of y = a^x across the line y = x. since log x and a^x are inverses of one another, composing them in either order gives the identity function.

We can have some observations about the logarithmic functions. From the graph, we can see that Logarithmic function is defined for positive values only and hence its domain is positive real numbers. The range is set of all real numbers. The graph always passes through (1, 0). The graph is increasing as we move from left to right. In the fourth quadrant, the graph approaches y-axis (but never meets it). It is also clear that the graphs of log base a x and a^x are mirror images of each other if y = x is taken as a mirror line.

Properties of Logarithmic Functions:
For any number x > 0 and y > 0, properties of base a logarithms are:
Product rule: log xy = log x + log y,
Quotient rule: log x / y = log x – log y,
Reciprocal rule: log 1 / y = -log y,
Power rule: log x^y = y log x.

Derivative of Logarithmic Functions: We use the following properties in the differentiation of logarithmic functions.
d/dx(e^x) = e^x
d/dx (log x) = 1/x.

Inverse of logarithmic functions : Since ln x and e^x are inverses of one another, we have  e^ln x = x ( all x > 0 ) ln ( e^x ) = x( all x ).

Logarithmic functions examples: Suppose we have to  Evaluate d/dx log base 10 ( 3x + 1 ).
d/dx log base 10 ( 3x + 1 ) = ( 1 / ln 10 ) .
( 1 / ( 3x + 1 ) ) d / dx ( 3x + 1 ) = 3 / [ ( ln 10 ) ( 3x + 1 ) ].

Evaluate integral log base 2 x /x dx.
Solution: integral log base 2 x / x dx = ( 1 / ln 2 ) integral ln x / x = ( 1 / ln 2 ) integral u du = ( 1 / ln 2 ) ( u^2 / 2 ) + C
= ( 1 / ln 2 ) [ ( ln x )^2 / 2 ] + C = ( ln x )^2 / 2 ln 2 + C.

Instantaneous rate of change of a function

Suppose we have a linear function such as y = 2x+3. The graph of this function is as follows:

Assume that to be a graph of the distance traveled by a car from home base, such that at time x = 0, the car is 3 miles from home. Now consider two points on the graph P(1,5) and Q(2,7). If we wish to find the rate of change of distance between these two points, we use the formula:
Rate of change = (y2-y1)/(x2-x1) = (7-5)/(2-1) = 2/1 = 2
That was fairly simple. That is because our graph was a straight line. Now suppose if the graph is not a straight line. And it is a curve instead.

The above graph as we see is not a straight line, but it is a curve. This time the co-ordinates of the points P and Q are (1,7) and (2,13) respectively. The average rate of change from P to Q can be found using the same formula above:
Average rate of change = (13-7)/(2-1) = 6/1 = 6. But we call this average rate of change since, it cannot be exact because the line between P and Q is not a straight line.
With this back ground let us now try to understand what is instantaneous rate of change. Now suppose the point Q moves closer and closer to point P, such that the distance between P and Q is infinitesimally small.

Therefore if co-ordinates of P are (x0, f(x0)) then those of Q would be (x0+h, f(x0+h)). Now, as Q moved closer and closer to P, the value of h goes on decreasing till it finally becomes 0 when Q coincides with P. That does not actually happen, h goes on decreasing to an infinitesimally small value. So we say that h tends to 0. Symbolically, h -> 0. Then the rate of change of the function f would be given as:
Rate of change = lim (h->0) [f(x+h) – f(x)]/[x+h – x] = lim(h->0) [f(x+h) - f(x)]/[h]
Stated above is the instantaneous rate of change equation. The term ‘rate of change’ now becomes ‘instantaneous rate of change’. We call it instantaneous because, at the instant when x = x0, the rate of change of the function is given by the limit:
instantaneous rate of change = lim(h->0) [f(x0+h) – f(x0)]/h

Instantaneous rate of change examples:
Find instantaneous rate of change of f(x) = x^2 at x = 4.
Ir = lim(h->0) [f(4+h) – f(4)]/h = lim(h->0)[16+8h+h^2-16]/h = lim(h->0)[8h+h^2]/h = lim(h->0)[h(8+h)]/h = lim(h->0)[8+h] = 8+0 = 8

Difference quotient of a function: Tangent lines and their slopes

This section deal with the problem of finding a straight line L that is tangent to a curve C at a point P. Before we go to learning that, let us make a few assumptions to start with (so as to avoid mathematical errors before we come to the end result). C is the graph of a function y = f(x) and this function is continuous over the interval (a,b). The co-ordinates of the point P are (x0,y0) and the point P lies on the curve C so that f(x0) = y0. Also we assume that P is not the end point of C. That means x0 is not equal to a or b. Therefore C extends to some distance on either sides of P.

A reasonable definition of tangency can be stated in terms of limits. If Q is a point on C different from P, then the line through PQ is called a secant line to the curve. This line rotates around P as Q moves along the curve.  If L is a line through P, whose slope is the limit of the slopes of these secant lines PQ as Q approaches P along C (see picture below), then we say that L is tangent to C at P.

Since C is the graph of the function y = (x), then vertical lines can meet C only once. Since P = (x0,f(x0)), a different point Q on the graph must have a different x-co ordinate, say x0+h, where h ? 0. Thus the co-ordinates of Q would be (x0+h, f(x0+h)) and the slope of the line PQ would be:
= (f(x0+h) – f(x0))/h, based on the formula for slope of line joining two points with co-ordinates (x1,y1) and (x2,y2). Slope = m = (y2-y1)/(x2-x1)

So for our line PQ, that would be:
m = (f(x0+h) – f(x0))/(x+h – x) = (f(x0+h) – f(x0))/h

The above expression is called the difference quotient formula or simply the difference quotient of a function f. Note that h can be positive or negative based on whether Q is to the right or to the left of P.

This method of finding the difference quotient is further applied in finding the derivative of functions in calculus. The basic limit definition of derivatives stems from this difference quotient.

Given the function y = f(x) and a point x = x0, or given a table of values of f(x) for various values of x, to evaluate the difference quotient and subsequently to simplify the difference quotient, is simple.

Derivative of Cos II

This function is known as differentiation of trigonometric function with use of calculus and various trigonometry rules.

Derivative of Cos Squared X
Derivative of any trigonometric function that is we have to differentiate the function one time. Here we have to find the derivative of Cos squared X. for this first we know the basic rules of differentiation. And also rules of trigonometry.
Derivative of Cos Squared X means first we write the function in (cosX)^2 , now we have to use chain rule . Take external term derivative from the function and then differentiate the internal term we get (2cosxsinx) with negative sign because one time differentiation of cos function is negative sine function.
Now by using trigonometry rule change the result means -2cosxsinx is replaced with -2sin2x. so finally we get derivative of cos squared x is( -2sin2x).

Derivative of Cos -1
Derivative of Cos-1 means we have to differentiate only cos function and cos-1 is a cos function only. So by differentiating that is derivative of cos-1 is sin-1 with negative sign. We have to differentiate only one time.

Derivative of Inverse Cos
For finding the derivative of inverse Cos we use inverse trigonometric rule and calculus rules. Inverse trigonometric function also called sometime as cyclometric function. They are inverse of trigonometric function with proper domains. These are also used as arcos, arcsin and etc.
Inverse laws are very restricted and we can’t go out of the domains. These are proper subsets of domains. Like if function y=square root of x then we write this function as y^2=x also. Similarly function y=arccos then we write this function as cosy=x also. And then differentiate the function.
Derivative of inverse Cos by differentiating we get 1/square root of (1-x^2).
                                              d/dx (arcos) =1/square root of (1-x^2)

Derivative of Cos X Squared
Derivative of Cos X Squared, we write this function also as y=(Cosx)^2, now we differentiate one time this function with respect to x.  Differentiate the external term we get 2 cosx now differentiate the internal term cosx with respect to x then we get sinx with negative sign. Thus total term by differentiating we get 2sinxcosx with negative sign.
We have to write the result in more accurate form. For this we have to use trigonometric rules. By using these rules we get 2sinxcosx in another form is sin2x.so we use this form.
Finally derivative of Cos X Squared we get 2sinxcosx or sin2x with negative sign.
                                     d/dx(cosx)^2=(-sin2x)

Intoduction to Partial derivative

Generally we come across with functions of two or more variables. For example, the area of a rectangle, with sides of length x and y is given by A = xy, which obviously depends on the values of x and y, and so it is a function of two variables. Similarly the volume V of a rectangular parallelepiped having sides x, y and z is given by V = xyz and so it is a function of three variables x, y and z. Generally functions of two, three, …, n variables are denoted by f (x, y), f ( x, y, z),…., f(x1, x2,…,xn) respectively. If u = f(x, y) is a function of two variables x and y, then x and y are called independent variables and u is called the dependent variable.

Partial derivatives: Let f(x, y) be a function of two variables x and y. The partial derivatives of f(x, y) with respect to x is defined as Lim h -> 0 f(x + h, y) – f(x, y) / h. Provided that the limit exists and is denoted by del f/del x. Thus, the partial derivative of f(x, y) with respect to x is its ordinary derivative w.r.t. x when y is treated as a constant. Similarly, the partial differentiation of f(x, y) with respect to y is defined as Lim k -> 0  f(x, y + k) – f(x, y) / k .Provided that limit exists and is denoted by del f/del y.

Thus, the partial differentiation of f(x, y) with respect to y is its ordinary derivative w.r.t. y when x is treated as a constant. The process of finding partial differentiation of a function is known as partial differentiation.

Let us see some Partial derivative examples: If f(x, y) = x^3 + y^3 – 3 axy, then Del f/del x = 3 x^2 + 0 – 3 ay = 3 ( x^2 – ay) [because y is treated as a constant].And del f/del y = 0 + 3 y^2 – 3 ax = 3 (y^2 – ax) [because x is treated as a constant].

Partial derivative symbols: Let f(x, y) be a function of two variables such that its partial differentiation (del f/del x) and del f/del y both exists. Then del f/del x and del f/del y are functions of x and y, so we may further differentiate them partial with respect to x or y. The partial differentiation  of del f/del x with respect to x and y are denoted by del^2 f/del x^2 and del^2 f/(del y del x). Similarly, the partial differentiation of del f/del y with respect to x and y are denoted by del^2 f/(del x del y) and del^2 f/del y^2.

A short note on inverse trig functions

Introduction:
We know that not every function as an inverse. A function has an inverse if and only if it is one to one and onto. As all trigonometric functions are periodic, they are all many to one type of functions. So technically, inverse of trig functions do not exist. But if we can suitably restrict the domain of the trigonometric function , then it becomes one to one and onto. Therefore with this modified domain the trigonometric function can have an inverse. Let us look at the following examples:

Inverse trig functions examples:

1. Inverse of sine function:
The sine function defined as follows: sin = {(x,y) | y = sin(x), x belongs to R, y belongs to [-1,1]} is an onto function. It is a many to one function. It is a periodic function with at period of 2belongs tobelongs to. But instead of R, if the domain is restricted to say, [-pi/2,pi/2], or [pi/2,3*pi/2], or [3pi/2, 5pi/2] etc, then it becomes one to one and still remains onto. Thus now we can define the inverse of sin function using any one of the above domains as follows: sin^(-1) = [(y,x) | y = sin(x), x belongs to [-pi/2,pi/2], y belongs to [-1,1]}, where “sin^(-1)” is the symbol for inverse sine function.

2.  Inverse of cosine function:
Just like how we defined the inverse of sine function, we can define the inverse of cosine function by restricting its domain as well. The domain restrictions can be made to suite our purpose. Therefore, inverse cosine function can be defined as follows: cos^(-1) = [(y,x) | y = cos(x), x belongs to [0,pi], y belongs to [-1,1]}

The other trigonometric function inverses can also be defined similarly.

Interrelations between inverse trigonometric functions:
Sin^(-1) x = cosec^(-1)(1/x), or cosec^(-1)(x) = sin^(-1)(1/x). The inverse functions of cos and sec  and the inverse function of tan and cot are related the same way.

Integral of inverse trig functions:
To find integral of inverse trigonometric functions, we use the method of integration by parts. We know that we follow the order LIATE (Logarithmic, Inverse Trigonometric, Algebraic, Trigonometric, Exponential function) for integration by parts. When we integrate inverse trigonometric functions, the inverse function becomes the u of the integration by parts and since there is no other function it is multiplied to, we take v = 1. Thus for example, if we were to integrate the function like tan^(-1)x using the integration by parts rule, then here u = tan^(-1)x and v = 1 and then integrate using integration by parts.

Trigonometric Identities

A function is a mathematical statement relating the different variables. When we assign the values for a set of independent variables, we get the definite value for the dependent variable.
Identity is a mathematical expression, which is valid for all the values of the variables. When the identity has terms involving the algebraic expression we call it as algebraic identity and the function involving the trigonometric expressions are called trigonometric identities.
Verifying Trigonometric identities:
Identities are mathematical statements that are valid for all the values of the variables. For example
(a +b)^2 = a^2 +2ab +b^2

The above expression is valid for all the values of ‘a’ and ‘b’. Trigonometry is the field of study involving triangles’ sides and angles. If the identity has any of the trigonometric functions, then it is called trigonometric identity. As the trigonometric functions are related to the angles, we substitute the angles in the functions of identities. We adopt the following steps to verify an identity.
Step 1: Choose an angle from the defined domain.
Step 2: Replace the variable by the chosen value
Step 3: Evaluate the function and simplify
Example: Sin^2 (x) + cos 2(x) =1
Step 1: For the value of x = 90
Step 2: Sin^2 (90) + cos^2 (90)
Step 3: 1+ 0 =1. Hence verified

Fundamental Trigonometric Identities
Trigonometry, a field of study involving the sides and angles of a triangle has a set of fundamental definition of trigonometric functions. Using the theorem of Pythagoras, we have three fundamental trigonometric identities called as Pythagorean identities, which are as follows.

In a triangle ABC:
(1) 1 = sin^2 (A) +cos^2 (A)
(2) 1+ tan^2(A) = sec^2(A)
(3) 1+ cot^2(A) = cosec^2(A)

Simplifying Trigonometric Identities
To simplify a given trigonometric identity, we always rely on the algebraic methods. Especially, we adopt PEMDAS/ BOADMAS in simplifying the identities.  In addition to this, we use the above three identities in simplifying the given trigonometric identities. At the same time, we ensure that the defined trigonometric identity is a valid one in the defined domain of variables.

Table of Trigonometric Identities:
The fundamental trigonometric identities are as follows
Reciprocal Identities:
Sec(A) = 1/cos(A) Cosec (A) = 1/ Sin(A) tan(A) = sin(A)/cos(A),   cot(A) = 1/ Tan(A)= cos(A)/sin(A)

Pythagorean Identities
(1) 1 = sin^2 (A) +cos^2 (A) (2) 1+ tan^2(A) = sec^2(A) (3) 1+ cot^2(A) = cosec^2(A)

Even-Odd Identities
(1) Sin (-A) = -sin(A) (2) cos(-A) = cos (A) (3) tan(-A) = -tan (A)
(4) Cosec (-A)= -cosec(A) (5) sec(-A)= -sec A (6) cot(-A) = -cot(A)

Standard deviation is a Measure of Dispersion

When we are dealing with data sets experimenter is interested to know two things about data set. Those are Measures of Central Tendency and Measures of Dispersion. Measures of Central Tendency are Mean, Median and Mode. Measures of Dispersion are Inter Quartile Range, Range, Mean deviation, Standard deviation and Variance. Measures of Central Tendency give the measures for center of the data. Measures of Dispersion give the measure for the variation in the data.

That is, it explains how much the data spread. Range is one type of measure of dispersion and it is the difference between maximum and minimum value in the data. It depends only on the extreme values and it neglects remaining values this is the drawback for this method. Inter Quartile Range is the difference between first and third quartiles. It gives the percentage of observations in between first and third quartile. In this case also it depends only on the first and third quartile values and neglecting remaining values. To come over from this drawback we can use Mean Deviation which includes each and every observation.

Main drawback of Mean Deviation is dealing with mathematical operations like differentiations and integrations are quite difficult. To come over from this drawback we can use Standard Deviation and Variance. Variance is the average of squared differences of the observations from their mean. Standard Deviation is the square root of the Variance. When we do not know standard Deviation for the population (It is a collection of huge similar type of items) then we have to estimate it by sample standard deviation. Symbol for Standard Deviation is’ ’. Symbol for Sample Standard Deviation is‘s’ Sample Standard Deviation Formula is .

Where ‘n’ is the sample size. Standard Deviation of the constant variable is zero. Constant variable means a variable which takes a fixed and single value. For example, a variable which takes only value 5 is called as constant variable and standard deviation of such variable is zero. For clear understanding of standard deviation, Standard Deviation Examples are discussed below. When we are Adding Standard deviations we cannot add them simply. First we have to square each individual standard deviation to make them variances. Now add these variances and take square root of this to add standard deviations. For subtracting standard deviations also we have to do the same thing. Standard Deviation Problems are not solvable directly first we have to find out the variance and then by taking square root of it we can get standard deviation. Standard Deviation Example, for the data 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Variance is 9.1667 and standard deviation is 3.02765. Mean of this data is 4.5 here the standard deviation value explains the average distance of the observations from its mean 4.5.


Know more about the online statistics help, Math Homework Help,online Math help. This article gives basic information about Standard deviation. Next article will cover more statistics concept and its advantages,problems and many more. Please share your comments.

Mode definition

Mode (statistics) is the value of the variable corresponding to the maximum of the ideal curve which gives the closest possible fit to the actual distribution of the frequency. It represents the value which is the most frequent or typical, the value which is, in fact, the fashion. The mode is sometimes denoted by writing the sign ? over the variants symbol, for example X? denotes the mode of the values X1,X2, …. Xn.

Mode formula:

It is evident that, mode is to be determined by inspection only. There is no stereotyped method listed for determination of the mode for a data set. It purely depends on the intuitions of the statistician or researcher. However there is an empirical relation between the mean, median and mode.
Mode = Mean – 3*(Mean – Median).
The above relation holds good with surprising closeness for moderately asymmetrical distributions.  Putting that in words, we say that the median lies one third of the distance mean to mode from the mean towards the mode.

Usually mode represents a single humped distribution unless specifically stated otherwise. When the distribution is of a complicated form, there may be more than one mode. Such distributions are therefore sometimes called multimodal. The mean and the median are still unique for such distributions.

What is mode for grouped frequency distribution:

Based on how we define mode, it is in fact difficult to determine the mode for grouped frequency distributions that are more common in practice. At max we can find the class with the maximum frequency. But beyond that it’s no use giving merely the mid value of the class interval into which the greatest frequency falls, for this is entirely dependent on the choice of the scale of the class intervals. It is again no use making the class interval very small to avoid error on that account, for the class frequencies will them become small and the distribution irregular. What we actually want to arrive is at the mid value of an interval for which the frequency would be a maximum, if the intervals could be made indefinitely small and at the same time the number of observations be so increased that the class frequencies should run smoothly. As the observations cannot, in a practical case, be indefinitely increased, it is evident that some process of smoothing out the irregularities that occur in the actual distribution must be adopted, in order to ascertain the approximate value of the mode.

Know more about the statistics help, Online Math help. This article give basic information about mode. Next article will cover more concept on statistics tutoring and its advantages and many more. Please share your comments.

Simplifying exponents

To understand simplification of exponents we first need to establish the rules of exponents.

Exponent rules:
1. b^m * b^n = b^(m+n)
2. b^m/b^n = b^(m-n)
3.(b^m)^n = b^mn
4.v(n&b^m ) = b^(m/n)

Exponentiation:

We know that multiplication corresponds to repeated addition. In the same way, exponentiation corresponds to repeated multiplication. In other words, exponentiation refers to the process of repeated multiplication. For example we can write, 4*4*4 as 4^3 or 5*5*5*5 = 5^4 etc. In general terms, b*b*b*b…. n times = b^n. Here, b is the base and n is called the exponent or the index.

b^2 is usually read as b squared. b^3 is read as b cubed; where as b^4 is read as ‘b raised to power 4’. In the same way b^(any other number) is read as ‘b raised to the power ______’.

Properties of exponents:
1. Exponent can be any real number.
2. When exponent is zero, the value of the term becomes equal to 1. That is to say that b^0 = 1
3. Exponent of one results in the base itself. So, b^1 = b.
4. ?(b?^(n)m) is not the same as b^(n^m ). ?(b?^(n)m) = b^mn where as b^(n^m ) = b^n^m.
5. When exponent is negative it is same as the positive exponent of the reciprocal of base. So, b^(-n) = (1/b)^n.

Rational exponents:

We saw above that exponent can be any real number. But for now we shall look at rational exponents only. A rational exponent would be of the type m/n. Therefore the number with rational exponent would look like this : b^(m/n). Based on the rules of exponents that we saw earlier, we can say that, b^(m/n) = v(n&b^m ). In other words it’s the nth root of b raised to power m. A number with a rational exponent may or may not itself be a rational number. For example, 4^(8/4) = 4^2 = 16. However, 3^(5/2) can be written as v(2&3^5 ) = v(3^4 * 3^1) = 3^(4/2) * 3^(1/2) = 3^2 * 3^(1/2) = 9 * v(3) = 9v(3) is an irrational number.

Solved examples:

1. Simplify: x^6 * x^5
Solution: x^6 * x^5 = x^(6+5) = x^11

2. Simplify: t^10/t^8
Solution: t^10/t^8 = t^(10-8) = t^2

3. Simplify: 5x^3/3x^5
Solution: 5x^3/3x^5 = (5/3)*(x^3/x^5) = (5/3) * (x^(3-5)) = (5/3) * x^(-2) = 5/3x^2

4. Simplify: (125x^2y^3z^2)^0
Solution: (125x^2y^3z^2)^0  = 1. That is because when exponent is zero, the term becomes = 1

What is a ratio

What is a ratio? A ratio is a comparison of two quantities by division. A ratio actually compares one thing happening to another. Ratios compares two or more amounts and are often expressed as fractions in simplest form or as decimals. Ratio can be written in three different ways:-

Example of a ratio

1. Using a colon like 3:2
2. Using a fraction like 3/2
3. Using the word “ to” like 3 to 2

Ratio Example: - Sam has 4 apples and 9 bananas. What is the ratio of his apples to bananas?
Solution: - Total numbers of apples are 4 and bananas are 9. SO the ratio will be 4:9.

Multiplying and dividing any ratio by same non- zero number makes no difference to the ratio. For example, the ratio 3:9 is equal to 1:3.
Two ratios that name the same number are equivalent ratios.  Equivalent ratios can be calculated by multiplying or dividing each term of the ratio by the same non - zero number.

For example: - If we have a ratio 2:7, multiplying both terms by 3 gives a new ratio 6:21
Hence, 2:7 and 6:21 are equivalent ratios.
If we have 12:3, if we reduce this fraction, we get 4:1
Hence 12:3 and 4:1 are equivalent ratios.
Now let us learn about ratio and rates. A rate is a ratio involving two quantities in different units. The rate 225 heartbeat/ 3minutes compare heartbeat to minutes. If the denominator is 1 then it is known as the unit rate. Therefore,
225 heartbeat/3 minutes = 75 heartbeat / 1 minute.
Hence, the unit rate is 75 heartbeats per minute.

Equivalent rates have the same value but use different measurements. We use equivalent rates to help us with unit conversions.

For example: - A jet flies 540 miles per hour. What is the rate in miles per minute?
Solution: - 540 miles/ 1 hour = 1hour/60 min
After simplifying, we get 9 miles per minute.

Bias

Let's learn about bias statistics in today's post.

There are four different types of bias in statistics:

• Spectrum bias
• Omitted variable bias
• Systematic bias
• Cognitive bias

Next time i will help you with the concept of statistics formulas.

Also you can avail help from expert online tutors. Not just in statistics but from an algebra tutor as well.

Do post your comments.