Introduction to parallel line extender:

Properties of parallel lines are the under the base of Euclid's parallel property. Two lines in a single plane that not even intersect or meet at any point then it is called as parallel lines. In other words Parallel lines are nothing but “A pair of lines in a plane which do not intersect or meet each other” then they are called parallel lines.

i.e. m1 = m2,

Where, m1 = slope of the first line.

m2 = slope of the second line.

Parallel Line Extender Problem:

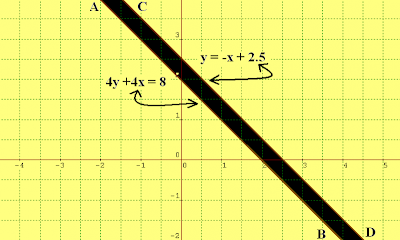
Example for parallel line extender: Define the equation parallel to 4y + 4x = 8 and the line extender, with point (6.5,4).

Solution:

Given 4y - 4x = 8 and the point (6.5, 4)

To detect the perpendicular line, we have to find slope first.

For finding the slope, we need to change the given equation into slope intercept form.

4y + 4x = 8

Add 4x on both side,

4y + 4x = 8

- 4x = -4x

4y = -4x + 8

Divide by 4 on both sides,

y = (-x + 2)

The obtained equation is in the form, y = mx + b

So, the slope from the obtained equation m = -1

From generally we know that the slope of parallel lines are equal i.e. m1 = m2

Here, m1 = -1

So, m2 = -1

The line equation is,

(y - y1) = m(x - x1)

(y - (4)) = -1 (x - ( 6.5))

(y - (4)) = (-x + 6.5)

Y - 4 = - x + 6.5

Subtract 4 on both sides,

y = -x + 2.5

Answer: Thus, the parallel line extender is given through the line y = -x + 2.5

Example for Parallel Line Extender:

Example for parallel line extender: Define the equation parallel to 2y - 2x = 4 and the line extender is gets through the point (-2, 0.5).

Solution:

Given 2y - 2x = 4 and the point (4, 3)

To detect the perpendicular line, we have to find slope first.

For finding the slope, we need to change the given equation into slope intercept form.

2y - 2x = 4

Add 2x on both side,

2y - 2x = 4

+ 2x = +2x

2y = 2x + 4

Divide by 2 on both sides,

y = (x + 2)

The obtained equation is in the form, y = mx + b

So, the slope from the obtained equation m = 1

From generally we know that the slope of parallel lines are equal i.e. m1 = m2

Here, m1 = 1

So, m2 = 1

The line equation is,

(y - y1) = m(x - x1)

(y - (3)) = 1 (x - (4))

(y - (3)) = (x - 4)

Y - 3 = x - 4

Subtract 3 on both sides,

y = x - 1

Answer: Thus, the parallel line extender is used to find the line y = x - 1